Signal Processing / Real-time FFT

This section requires mastering the concepts of sampling and DSP.

Fast Fourier Transform vs Fourier transform

The interest in the Fourier transform lies in its ability to analyze and manipulate signals in various domains. By breaking down a signal into its constituent frequencies, it enables analysis and processing in various fields such as signal processing, communications, and image processing.

The Fast Fourier Transform (FFT) is an algorithm that computes the Discrete Fourier Transform (DFT) of a sampled signal.

FFT transforms a signal from its time (or spatial - for images) domain into the frequency domain. It accomplishes this by recursively dividing the DFT into smaller DFTs, significantly reducing computation time compared to the standard DFT calculation, making it a fundamental tool for spectral analysis and signal processing applications.

Fourier Transform calculation

The Fourier transform of a function \(f(t)\) is given by the following formula:

\[\hat{f}(\omega) = \mathcal{F}\{f(t)\}(\omega) = \int_{-\infty}^{\infty} f(t) \cdot e^{-i\omega t} \, dt\]

Fourier transforms have a lot of remarkable properties. These properties are not addressed in this document, but you can find a lot of ressources on the Internet.

DFT calculation

Based on this sampling, the DFT can be calculated by integrating

\[X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i\frac{2\pi}{N} kn}, \quad k = 0, 1, \ldots, N-1\]

Sampling and FFT algorithm

On cherche ici à calculer le spectre d’un signal analogique à l’aide d’une carte Nucléo.

Il est alors nécessaire d’utiliser une acquisition du signal d’entrée analogique, à un rythme régulier, compatible avec le critère de Shannon. La programmation de ces cartes par le biais du système d’exploitation embarqué MBED limite énormément les capacité d’échantillonnage (temps de conversion autour de 25us). Ici, on utilise un Ticker qui appelle la fonction sample à intervalle régulier.

Les éléments convertis, sur une période donnée, sont alors stockées dans un tableau. Ici, on récupère 256 éléments, dans le tableau Input à un rythme de 40us chacun (fréquence de 25 kHz). Pour optimiser les calculs, il est préférable d’utiliser un nombre d’éléments qui est une puissance de 2, l’ensemble des données et des éléments séquentiels d’un microcontroleur fonctionnant en binaire.

Vient ensuite la partie calculatoire où ici on utilise un algorithme particulier de calcul de la transformée de Fourier appelé FFT (Fast Fourier Transform). Cet algorithme est déjà implémenté dans la bibliothèque dsp.h de MBED. Il se fait dans la partie principale du code mais n’est exécuté que lorsque le sémaphore trig n’est pas bloqué par l’échantillonnage des N valeurs.

Enfin, l’affichage se fait par l’intermédiaire d’un convertisseur numérique-analogique à un rythme de 1 échantillon toutes les 10us environ. Une première impulsion à 3.3V de durée 20us permet de synchroniser l’affichage. Puis les différentes valeurs du spectre sont régulièrement converties par le CNA.

FFT with Nucleo

http://lense.institutoptique.fr/nucleo-obtenir-le-spectre-dun-signal-en-temps-reel-4/

Algorithm

Creating an MBED6 project

CMSIS-DSP library

Adding a library by right-click on the active project and select

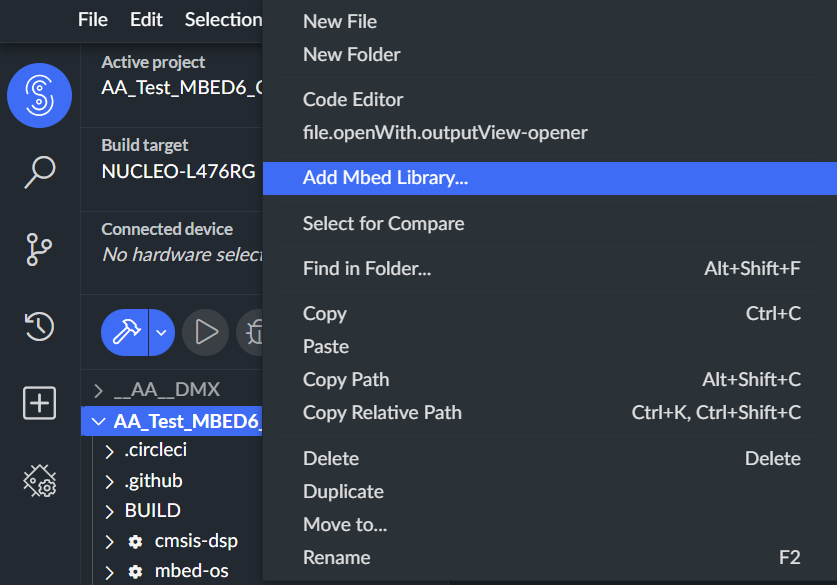
In the popup window, paste the GitHub link : https://github.com/ARM-software/CMSIS-DSP then click Next

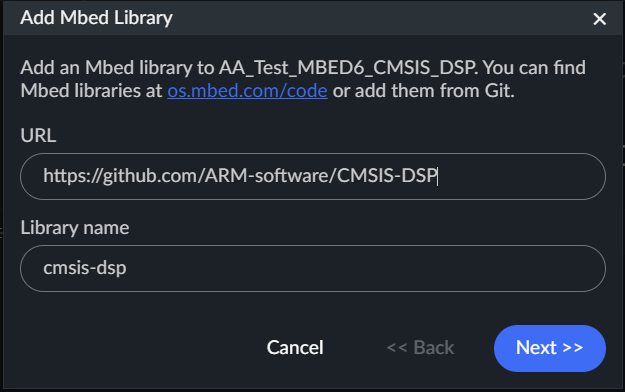
Select the version of the library then click Finish.

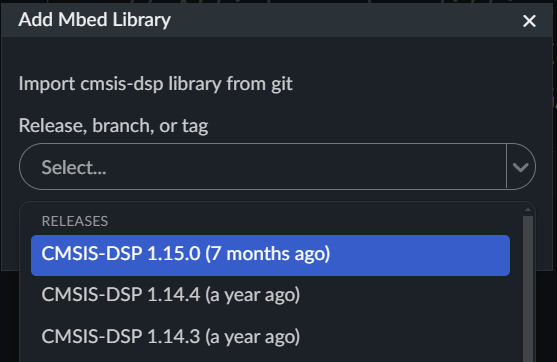
The library is adding in the project.

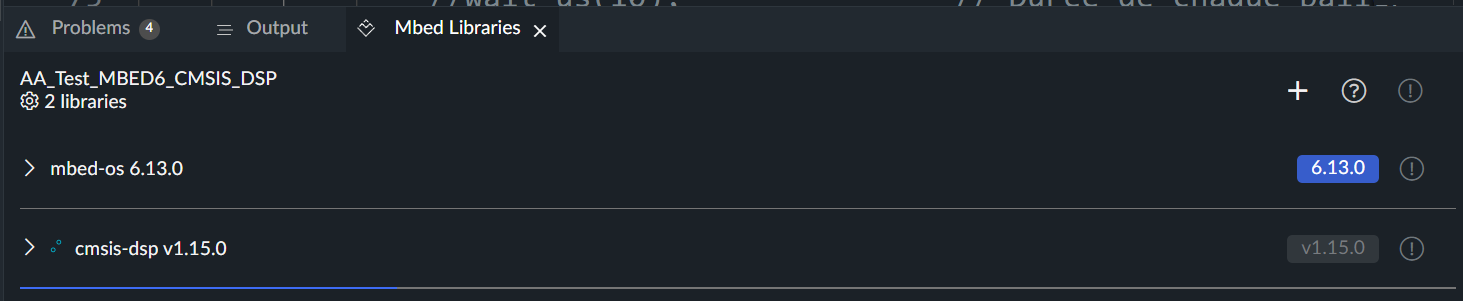
Adding a .mbedignore file

Adding a new file by right-click on the active project and select New File.

Create a .mbedignore file.

cmsis-dsp/Examples/*
cmsis-dsp/PythonWrapper/*
cmsis-dsp/Scripts/*
cmsis-dsp/Testing/*
cmsis-dsp/ComputeLibrary/*

cmsis-dsp/Source/BasicMathFunctions/BasicMathFunctions.c
cmsis-dsp/Source/BasicMathFunctions/BasicMathFunctionsF16.c
cmsis-dsp/Source/BayesFunctions/BayesFunctions.c
cmsis-dsp/Source/BayesFunctions/BayesFunctionsF16.c
cmsis-dsp/Source/CommonTables/CommonTables.c
cmsis-dsp/Source/CommonTables/CommonTablesF16.c
cmsis-dsp/Source/ComplexMathFunctions/ComplexMathFunctions.c
cmsis-dsp/Source/ComplexMathFunctions/ComplexMathFunctionsF16.c
cmsis-dsp/Source/ControllerFunctions/ControllerFunctions.c
cmsis-dsp/Source/DistanceFunctions/DistanceFunctions.c
cmsis-dsp/Source/DistanceFunctions/DistanceFunctionsF16.c
cmsis-dsp/Source/FastMathFunctions/FastMathFunctions.c
cmsis-dsp/Source/FastMathFunctions/FastMathFunctionsF16.c
cmsis-dsp/Source/FilteringFunctions/FilteringFunctions.c
cmsis-dsp/Source/FilteringFunctions/FilteringFunctionsF16.c
cmsis-dsp/Source/InterpolationFunctions/InterpolationFunctions.c
cmsis-dsp/Source/InterpolationFunctions/InterpolationFunctionsF16.c
cmsis-dsp/Source/MatrixFunctions/MatrixFunctions.c
cmsis-dsp/Source/MatrixFunctions/MatrixFunctionsF16.c
cmsis-dsp/Source/QuaternionMathFunctions/QuaternionMathFunctions.c
cmsis-dsp/Source/StatisticsFunctions/StatisticsFunctions.c
cmsis-dsp/Source/StatisticsFunctions/StatisticsFunctionsF16.c
cmsis-dsp/Source/SVMFunctions/SVMFunctions.c
cmsis-dsp/Source/SVMFunctions/SVMFunctionsF16.c
cmsis-dsp/Source/TransformFunctions/TransformFunctions.c
cmsis-dsp/Source/TransformFunctions/TransformFunctionsF16.c
cmsis-dsp/Source/WindowFunctions/WindowFunctions.c

Caution

Be careful to let a blank line at the end of this file.

Main program

Sampling application

#include "mbed.h"

DigitalOut myled(D3);
AnalogIn   myADC(A1);
AnalogOut  myDAC(D13);
Ticker     timer;

void sample(){
        myled = !myled;
        float val_in = myADC.read();
        myDAC.write(val_in);
}

int main() {
        timer.attach(&sample, 40us);    //40us 25KHz sampling rate

        while(1) {
                thread_sleep_for(10);
        }
}

Final code

#include "mbed.h"
#include "arm_math.h"
#include "arm_common_tables.h"
#include "arm_const_structs.h"

#define SAMPLES                 512
/* 256 real party and 256 imaginary parts */
#define FFT_SIZE                SAMPLES / 2
/* FFT size is always the same size as we have samples, so 256 in our case */
#define OUTPUT_GAIN             10.0
/* Gain on the output values - for better display */

float32_t Input[SAMPLES];
float32_t Output[FFT_SIZE];

bool      trig=0;         // sampling blocking semaphore
int       indice = 0;

DigitalOut myled(D3);
AnalogIn   myADC(A1);
AnalogOut  myDAC(D13);
Ticker     timer;

void sample(){
        myled = 1;
        if(indice < SAMPLES){
                Input[indice] = myADC.read() - 0.5f;
                // Real part NB removing DC offset
                Input[indice + 1] = 0;
                // Imaginary Part set to zero
                indice += 2;
        }
        else{ trig = 0; }
        myled = 0;
}

int main() {
        float maxValue;            // Max FFT value is stored here
        uint32_t maxIndex;         // Index in Output array where max value is

        while(1) {
                if(trig == 0){
                        timer.detach();
                        // arm_cfft_sR_f32_lenXXX, where XXX is the samples number, here 256
                        arm_cfft_f32(&arm_cfft_sR_f32_len256, Input, 0, 1);

                        // FFT calculation and storage of the magnitude of the complex FFT values in the Output array
                        arm_cmplx_mag_f32(Input, Output, FFT_SIZE);
                        Output[0] = 0;

                        // Analog display of the FFT
                        myDAC=1.0f;     // Sync pulse
                        wait_us(10);
                        myDAC=0.0f;
                        // Display all the values
                        for(int i=0; i < FFT_SIZE; i++){
                                myDAC.write(OUTPUT_GAIN * Output[i]/FFT_SIZE);
                        }
                        myDAC=0.0f;

                        // Restart sampling
                        trig = 1;
                        indice = 0;
                        timer.attach(&sample,40us);    //40us 25KHz sampling rate
                }
        }
}